| Главная страница | Авторский информационный ресурс врача-исследователя Воробьева К.П. |
|---|---|
| Публикации | |
| Эта статья была впервые опубликована: | на сайте фирмы ПалларЛТД (Винница) http://www.pallar.ua/index_r.htm, 29.11.2002г. |
| Соавторы | Паламарчук Е.А. Вінницький державний агарний університет, evgen.pal@gmail.com |
| Научный вклад соавторов в исследование | Воробьев К.П.: идея исследования и обозначение сути проблемы, проведение экспериментов с программным иммитатором сигналов Паламарчук Е.А.: создание иммитатора гармонических сигналов, теоретическое обоснование корректности решения проблемы |
К ВОПРОСУ О СТАНДАРТИЗАЦИИ МЕТОДОВ СПЕКТРАЛЬНОГО АНАЛИЗА КАРДИОИНТЕРВАЛОГРАММ
Часть 1. Воробьев К.П. к.м.н, (врач и исследователь), г.Луганск,
Преамбула
Оценка вариабельности сердечного ритма (ВРС) относится к новым диагностическим технологиям, которая начала активно выходить за пределы научных лабораторий. Этот метод диагностики становится одним из важнейших клинических тестов в оценке, как вегетативного статуса организма, так и интегральных характеристик функционального состояния.
Любому исследователю хочется иметь проверенный и точный инструмент. В клинической практике, при диагностике различных состояний необходима повторяемость результатов функциональных исследований и их четкая метрологическая характеристика.
Автор этих строк исследователь и практик, который уже много лет использует ВРС как инструмент познания и как диагностический тест оценки эффективности гипербарической оксигенации.
Общение с коллегами, изучение литературы и собственные изыскания показывают, что при анализе ВРС существует множество нерешенных проблем. Одна из них, наиболее важная, – это стандартизация математического аппарата вычисления спектральных характеристик кардиоинтервалограмм. По этому поводу разработчики соответствующего российского стандарта пишут: «Сравнимость записей и результатов анализа ВСР означает возможность сопоставления данных, получаемых в различных клиниках и учреждениях с помощью разных типов аппаратуры и разных программных средств» [Методические рекомендации по анализу вариабельности сердечного ритма при использовании различных электрокардиографических систем (анализ “коротких” записей), с.20]
Нас не удовлетворяют существующие алгоритмы вычисления спектральных характеристик. Более правильно предлагать в стандартах не алгоритм высокой математической абстракции, а конкретную блок схему вычисления спектра ВРС. Возможно это «покоробит» математические умы, но врачу сейчас необходим инструмент и подробная инструкция к нему.
Мы предполагаем, что такое подробное описание математического аппарата спектрального анализа может нанести некоторый урон производителям программ. Очевидно, что это не главная беда. А уважаемые коммерсанты заработают на самих приборах и удобных программных оболочках. Кроме того, в настоящее время главным становится не вычислить определенный показатель, а правильно и наглядно его представить в сопоставлении с другими характеристиками – а это и есть основная задача коммерческих программных комплексов анализа ВРС.
Прозрачность математического аппарата оценки спектра ВРС позволит исследователям говорить на одном языке, а врачам - пользоваться стандартными диагностическими методиками.
Эти идеи зрели давно и обрели более четкие очертания во время первой Международной конференции по ВРС (институт геронтологии, Киев, 26-27 октября) при обсуждении существующих стандартов ВРС. Вместе с математиком, одним из авторов диагностических программ CARDIO ( http://www.pallar.com.ua/ ) Е.А.Паламарчуком мы в течение более месяца вели интенсивную переписку по электронной почте. Я учился некоторым понятиям математики, а Евгений Анатольевич с удивлением узнавал, что некоторые банальные математические истины могут быть не понятны врачу. Мы протестировали разные программы, в каждой из них нашли ошибки и улучшили их, создали тестовые программы для проверки существующих. Первый этап этой работы закончен, и мы хотим поделиться ее результатами.
Общие понятия спектрального анализа кардиоинтервалограммы
Мы не будем здесь говорить об азах спектрального анализа кардиоинтервалограмм – это не является нашей задачей. Эту информацию Вы сможете получить в самых различных источниках, в которых нет недостатка. Поговорим о другом - о том как понять, что в этих самых источниках не пишется.
Спектральный анализ сигналов достаточно сложная математическая технология, в которой пока не поставлены все точки. Разделы по этому вопросу в руководствах по анализу ВРС пишут чаще всего математики. Многие вещи для них очевидны, а для врача нет. Мы постараемся разобраться в смысловом содержании спектра ВРС, рассмотрим логику получения расчетных характеристик спектра из массива спектральных характеристик кардиоинтервалограммы.
Чаще всего для спектрального анализа ВРС используется быстрое преобразование Фурье – так называемое БПФ. После обработки кардиоинтервалограммы образуется ряд спектральных характеристик, которые состоят из двух характеристик: частоты и амплитудного значения спектра. Частота выражается в герцах, амплитуда в миллисекундах. Ряд значений спектра дискретный, то есть характеризует не все присущие сигналу частоты, только выборочные, что является слабым местом метода БПФ.
В соответствии с известным международным стандартом принято соглашение о разделении всего измеряемого диапазона на четыре: ультранизкие частоты ( -<0,003 Гц), очень низкие частоты (0,003-0,04 Гц), низкие частоты ( 0,04-0,15 Гц) и высокие частоты ( 0,15-0,4 Гц). Клиническое значение определено, в основном, для последних трех диапазонов. О них мы и поговорим.
Типичный график спектрального анализа кардиоинтервалограммы представлен на рис.1
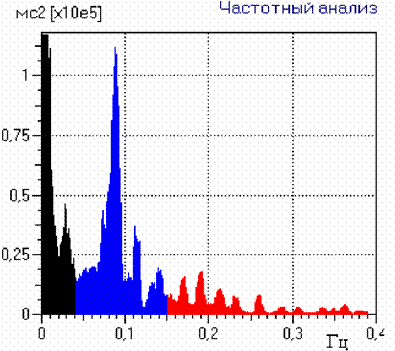 |
| Рис.1 Типичное представление спектрального анализа кардиоинтервалограммы . |
На этом графике тремя цветами обозначены характеристики соответствующих трех исследуемых диапазонов. Для придания кривым графика благообразный вид иногда используют специальные виды обработки, которые позволяют получить более плавный вид огибающей кривой графика.
Наши исследования
От данного представления спектра кардиоинтервалограммы мы перейдем к другому. Во всех последующих примерах на рисунках будут представлены: исходная кардиоинтервалограмма, ее статистические характеристики (максимальное, минимальное среднее и дисперсия ряда кардиоинтервалов), храктеристики мощностей спектральных диапазонов и первые два десятка характеристик спектра (номер спектрального диапазона, значение мощности в этом диапазоне в мс 2 и частота, которой соответствует данный диапазон).
Для дальнейшего описания спектра мы использовали специальную тестовую выборку кардиоинтревалов с заведомо известными характеристиками, которые указаны в подписях к рисункам. Тестовые выборки анализировались специальной программой, которую подготовил автор для данных исследований. Тестовые выборки создавались программой, которую подготовил Е.А.Паламарчук.
На рис 2 показаны результаты обработки тестовой выборки.
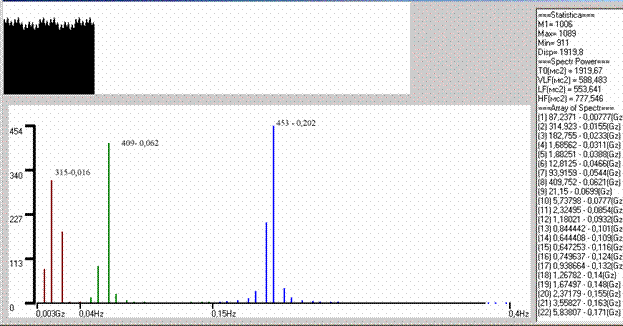 |
| Рис.2 Тестовый пример с параметрами: VLF =600 ms 2 ( f =0,015); LF =600 ms 2 ( f =0 ,06 ); LF =800 ms 2 ( f =0,2); При объеме выборки 128 число дискретных диапазонов спектра в диапазоне 0,003-0,4 = 51. |
На этом рисунке показаны результаты анализа выборки из 128 кардиоинтервалов. Первое значение спектра соответствует 0,0077 Гц, что не позволяет корректно охарактеризовать весь диапазон .
Это значение соответствует времени, в течение которого производился набор этих 128 кардиоинтервалов (1/0,0077Гц = 128,7 сек). Для характеристики более низкой частоты необходимы более длительные выборки. На следующем рисунке представлен анализ той же тестовой кардиоинтервалограммы, но в два раза больше по объему выборки (Рис.3), т.е 256 кардиоинтервалов.
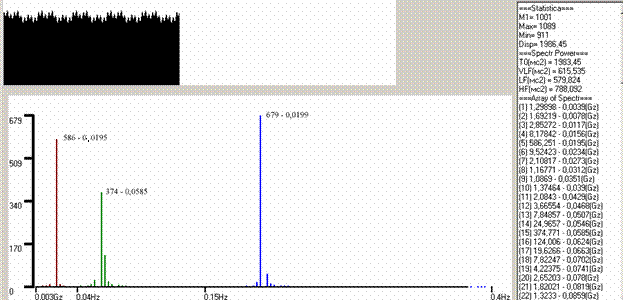 |
| Рис.3 Тестовый пример с параметрами: VLF =600 ms 2 ( f =0,015); LF =600 ms 2 ( f =0,06); LF =800 ms 2 ( f =0,2); При объеме выборки 256 число дискретных диапазонов спектра в диапазоне 0,003-0,4 = 102 |
В этом примере самая низкая измеряемая частота равна 0,0039 Гц, что соответствует (1/0,0039) 256,4 секундам длительности исследуемой выборки. Но это также недостаточно чтобы корректно охарактеризовать весь очень низкочастотный диапазон.
Обсуждение результата исследования
Теперь давайте на последних двух примерах разберемся в некоторых вопросах.
Как считается мощность соответствующего диапазона?
В международном стандарте предусмотрен анализ, пятиминутных выборок. Пять минут составляют 300 секунд, тогда минимальная анализируемая частота будет соответствовать 0,00333Гц. То есть фактически соответствует самому низкочастотному диапазону (0,003 Гц). Предусмотрено, что изучаемые частоты увеличиваются с шагом 0,003 Гц. Для того чтобы достичь частоты 0,4 Гц необходимо (0,4-0,003)/0,003=133 шага. Мощность соответствующего частотного диапазона характеризуется простой суммой спектральных мощностей в диапазонах с шагом 0,003 Гц. Это классика.
Теперь давайте посмотрим, как нарушение классики влияет на точность результатов.
Во втором случае (рис.3) мы проанализировали почти полную, соответствующую классике, выборку, в первом (рис .2) - явно недостаточную выборку. Мы также сделали еще три эксперимента на тестовой кардиоинтервалограмме с выборками 64, 32 и 16 кардиоинтервалов. Сравним результаты измерения спектральных мощностей в трех диапазонах (табл.1)
Таблица 1. Результаты спектрального анализа тестовой кардиоинтервалограммы при различных объемах выборки
| Выборка (длительность) | Общая мощност ь( мс 2 ) | VLF (мс 2 ) | LF (мс 2 ) | HF (мс 2 ) | К-во частотных шагов |
| 600 | 600 | 800 | |||
| 256 (256,4 сек) | 1983 | 615 | 579 | 788 | 102 |
| 128 (128,7 сек) | 1919 | 588 | 553 | 777 | 51 |
| 64 (64,1 сек) | 1976 | 590 | 587 | 798 | 25 |
| 32 (32 сек) | 1425 | 55 | 612 | 757 | 13 |
| 16 (16 сек) | 1021 | 0 | 340 | 680 | 6 |
Мы видим, что полученные результаты очень близки к заданным. Погрешность наших измерений составила до 8%, даже для выборки объемом 64 кардиоинтервала. Последний факт можно объяснить тем, что в диапазоне VLF была задана основная частота 0,015 Гц, что соответствует 66 секундам, т.е. довольно близко к первому частотному шагу измерения при длительности выборки 64 секунды.
Известно, что при анализе коротких выборок чаще всего изучают характеристики LF и HF, поэтому для их изучения согласно нашим экспериментам вполне достаточно выборок кардиоинтервалов длиннее, чем 25 секунд (0,04 Гц). Правда надо учесть, что с уменьшением длительности выборки падает точность измерения, так как количество частотных шагов, на которых измеряются мощности спектра уменьшается пропорционально снижению времени выборки (см. левый столбец табл.1). Продемонстрируем последнее замечание на реальной кардиоинтервалограмме (рис.4 и 5).
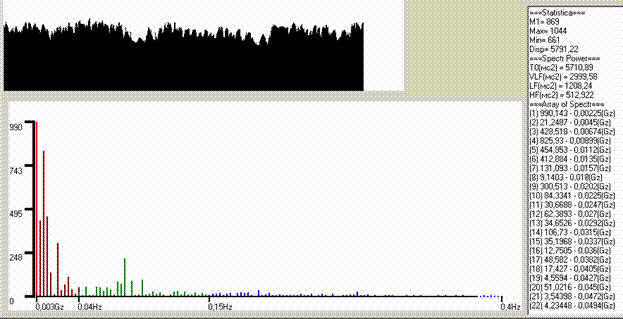 |
| Рис.4 Реальная кардиоинтервалограмма у больной с начальными проявлениями диабетической полинейропатии. При объеме выборки 512 число дискретных диапазонов спектра от 0,003-0,4 = 178 |
 |
| Рис.5 Реальная кардиоинтервалограмма у больной с начальными проявлениями диабетической полинейропатии. При объеме выборки 128 число дискретных диапазонов спектра от 0,003-0,4 = 46. |
Число дискретных диапазонов измерения мощности спектра уменьшилось в 4 раза при уменьшении объема выборки с 512 до 128, но значения мощностей осталось сопоставимым (надо учесть, что в реальной записи последующие после 128 кардиоинтервалы не могут повторять предыдущие, т.е. соответственно не могут совпадать мощности спектров).
Заключение
Эти эксперименты были проведены врачом при консультативной поддержке математика. Они показывают, что метод БПФ позволяет получить удовлетворительные повторяемые результаты. Мы также надеемся, что для некоторых коллег чтение этого материала позволило разобраться в некоторых тонкостях расчета спектральных характеристиках ВРС.
Метод БПФ по отношению к кардиоинтервалограмме имеет определенную математическую некорректность, т.к. по оси абсцисс откладывается не время а номер последуюшего кардиоинтервала. Эту неточность пытаются устранить российские коллеги, предлагая в своем проекте стандарта анализировать методом БПВ не кардиоинтервалограмму, а функцию – x(t), которая строится из исходной кардиоинтервалограммы методом сплайновой кубической интерполяции, при квантовании функции x(t) с шагом 250 мс.
Мы пробовали этот метод, но не получили очевидных преимуществ. Возможно мы что - то сделали неточно. Но пока авторы стандарта не предложили соответствующие тестовые примеры и более подробный алгоритм расчета спектра, трудно отдать предпочтение их выбору. А инструмент для врача и исследователей необходим сегодня. Поэтому мы пока предлагаем использовать проверенный метод, который позволяет получить повторяемые результаты.
Для того чтобы метод был действительно повторяемый необходим подробный алгоритм расчета характеристик спектра. Эту работу любезно согласился выполнить специалист, которому и предоставляем слово.
Константин Петрович Воробьев, к.м.н., заведующий отделением гипербарической оксигенации Луганской областной клинической больницы.
29.11.02
Часть 2. Паламарчук Е.А. к.т.н, доцент, г. Винница,
Спасибо. Итак, давайте вначале разберемся со временн`ой нормировкой . Вопрос заключается в том, сколько точек (или сколько RR-интервалов) должно быть во входном массиве? Оказывается, что не имеет значение их количество, а важно, какое они образуют время обследования . В сумме это время должно составлять около 333 секунд . И вот почему. Нижняя граница спектра VLF составляет 0.003 Hz . Расчитаем время снятия ритмограммы, которое будет соответствовать этой частоте. Для этого поделим 1 sec/0.003 Hz = 333 sec. Следует отметить также, что при спектральном преобразовании 0.003 Hz будет соответствовать еще и разности частот между соседними точками спектра, т.е. определять частотный шаг. Здесь же отметим физичекую сущность первого элемента спектра. Это постоянная составляющая (нулевая частота). Она несет информацию о средней ЧСС за обследуемый период. В расчетах спектральной мощности ее учитывать не надо. Теперь расчитаем, какая должна быть минимальная размерность спектрального массива. В общем случае она зависит от количества сердечных сокращений за 333 сек, а также алгоритма применемого спектрального преобразования. К примеру, предполагая, что частота сердечных сокращений не будет превышать 90 уд.\мин, получим, что за 333 секунды произойдет около 333/60*90=~500 сердечных сокращений. Таким образом, размерность исходного массива с RR-интервалами должна быть не менее 500 точек . Будем использовать алгоритм быстрого преобразования Фурье (БПФ). Его особенностью является не только малое время преобразования, но и то, что размерность спектрального массива должна быть кратна степени двойки. Таким образом, ближайшая размерность в данном случае составит 512 точек. Однако при БПФ всегда формируется симметричный спектр , состоящий из двух одинаковых, но зеркально расположенных относительно нулевой частоты спектральных частей. Следовательно, размерность частотного массива должна быть в два раза больше выбранной. Т.е. не в данном случае - не менее 1024 точек. Невыполнение этого условия приведет к катастрофическому искажению результатов пребразования. Теперь, учитывая, что частотный шаг мы ранее расчитали и он составил 0.003 Hz, можно легко определить, где в спектральном массиве будут находиться частотные области VLF , LF и HF . Так, для VLF-части спектра (0.003-0.4 Hz) будуть соответствовать точки от 2 (Внимание! В нашем случае элементы нумеруются от 1. Поэтому 1 точке будет соответствовать нулевая частота) до 13 -ой спектрального массива, для LF-части спектра (0.4-0.15 Hz) -от 14 до 50 точки, а HF-части (0.15-0.4 Hz) - от 15 до 133 точки. Имея расчитанный спектр и границы частоных зон (VLF, LF, HF), легко получить спектральные мощности, подсчитав сумму квадратов амплитуд спектральных составляющих в каждой частотной области (см. текст программного модуля spec_lib ниже). Второй проблемой является амплитудная нормировка выбранного спектрального преобразования . Дело в том, разные алгоритмы вычисления спектров могут давать различные передаточные коэффициенты (не следует путать с соотношением спектральных составляющих). Говоря иначе, необходимо иметь некий коэффициент преобразования , который бы обеспечивал соответствие расчитанной мощности спектра ее реальным значениям . Напрашивается мысль, что необходимо иметь некое поверочное средство-эталон, с помощью которого можно было бы верифицировать используемый алгоритм спектрального преобразования. Такая задача решается весьма просто, если учесть, что спектральные преобразованя - это линейные преобразования, где справедлив принцип суперпозиции. Он означает, что любой сигнал может быть представлен определенным набором гармоник (спектральных составляющих) или, наоборот, эти гармоники однозначно могут быть преобразованы в исходный сигнал. Из этого вытекает, что в качестве поверочного средства можно использовать обычные гармонические колебания с заданной частотой и амплитудой (Или их смесь). То есть, оцифровав, например, гармонику с и заданной амплитудой и частотой 0.01 Hz, мы получим в спектре спектральную составляющую с частотой 0.01 Hz и мощностью, соответствующей амплитуде входного сигнала. Все остальные гармоники спектра будут равны нулю. Среднеквадратическая мощность (P) синусоидального сигнала (гамоники) связана с ее амплитудой (A) как P=A*A/2 . Таким образом, если мы, оцифруем две гармоники, то в спектральной области появятся две независимые друг от друга составляющие. Каждая из них будет иметь мощность, опеделяемую среднеквадратической мощностью своего гармонического сигнала. Из сказанного следует, что мы имеем право оперировать суммой любого числа гармоник, где каждая их них определяет свою спектральную составляющую. В сущности любая ритмограмма и есть набор гармоник со своими амплитудами и фазовыми соотношениями. Таким образом, используя три гармоники, размещенные в частотых областях VLF, LF и HF мы имеем возможность моделировать любые виды частотных соотношений для проверки адекватности выбранного матаппарата частотного преобразования. Здесь находится программа-иммитатор (HRV_Imit.EXE) , которая реализует описанный выше принцип. Она позволяет сформировать оцифрованную смесь из трех любых частот лежащих в диапазоне (VLF..HF) с произвольными мощностями вывести ее в текстовый файл export.rg . Структура файла отвечает российскому стандарту формата записи ритмограмм, где в каждой строке записывается по одному RR-интервалу в ASCII-формате. Такой файл легко импортировать в любую верифицируемую программу. Ниже приведен код программного модуля, реализующего обработку ритмограммы с использованием алгоритма БПФ. Этот модуль использован в в тестовой программе (checkFFT.EXE ) , обрабатывающей текстовый файл ритмограммы с описанной выше структурой. Программу checkFFT.EXE можно также использовать для обработки ритмограмм, экспортированных и из других программ. В заключение хочу сказать, что если говорить об использовании медицинского программного обеспечения в научных исследованиях и практике, то его обязательным критерием должна быть возможность импорта\экспорта биосигналов в общедоступном формате (см. выше). Только тогда будет обеспечена возможность контроля правильности функционирования матаппарата тех или иных программ, а также проведения сопоставимых научных и медицинских исследований на программных продуктах от разных производителей. |
unit spec_lib; {модуль, що реалізує перетворення ритмограми на спектр і обрахунок спектральних параметрів } {максимум спектру} AmplMasht := SSS^[ NumPoint ].re; |